TP: Visualisation de la période de Pisano

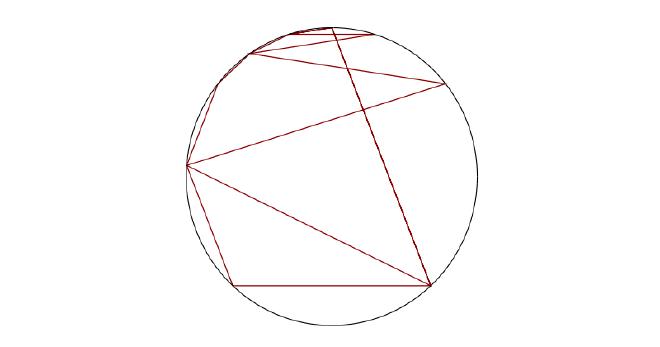
Ce sujet PDF est inspiré d’une superbe vidéo de Jacob Yatsko dans laquelle les nombres de Fibonacci modulo \(p \in \mathbb{N}^*\) sont placés sur un cercle. À partir d’un certain rang (qui dépend de \(p\)), la suite est périodique; ce rang est appelé période de Pisano. L’objectif du TP est de reproduire cette visualisation sur le cercle avec Scilab.

Étant donné que le sujet s’adresse aux élèves en fin de première année de formation GEII à l’IUT, la notion de modulo n’est pas supposée connue, donc elle est présentée rapidement. En accord avec l’esprit du cours Outils Logiciels, les questions mélangent raisonnements mathématiques et programmation. Notamment, on se sert de la programmation pour calculer la période de Pisano. Ce sujet permet en outre d’introduire de la notion d’erreur d’arrondis. En effet, comme les termes de la suite de Fibonacci croissent de manière exponentielle, on ne peut pas se contenter de les calculer puis de les prendre modulo \(p\). Il faut faire tous les calculs modulo \(p\).

Les questions primordiales sont indiquées avec un cœur et les questions standard avec un triangle. Les élèves qui souhaitent approfondir le sujet et leurs connaissances mathématiques (ou simplement améliorer leur note) peuvent répondre aux questions indiquées par un symbole de pique. De cette manière, les connaissances attendues par l’étudiant sont rendues explicites.

Il est à noter que ce sujet a été pensé comme un mini-projet en temps libre sur plusieurs semaines, et donc certaines questions sont difficiles. Les élèves sont encouragé-e-s à soliciter les enseignant-e-s pour se débloquer.